Law of Cosines Calculator

Created by
Eon CalculatorWhat is the Law of Cosines?
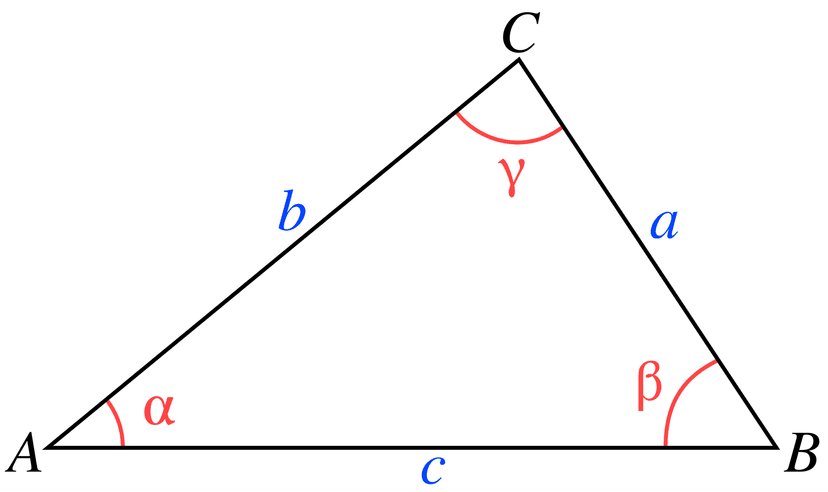
What are Law of Cosines formula
The law of cosines allows you to calculate unknown sides or angles in any triangle using this main formula:
Where;
a, b, and c are the sides of a triangle and γ is the angle opposite side c.
The Law of Cosines can be written in three different forms depending on which side or angle of the triangle you are solving for;
To find side a:
Where α is the angle opposite side a.
To find side b:
Where β is the angle opposite side b.
If you know the values for all three sides and you need to find an angle, rearrange the formula to solve for cosine:
To find angle γ;
Then use the inverse cosine function (cos⁻¹) to find the angle:
| Use Case | Know Values | Formula | Find |
|---|---|---|---|
Side a | b, c, ∠α | a² = b² + c² - 2bc⋅cos(α) | Side a |
Side b | a, c, ∠β | b² = a² + c² - 2ac⋅cos(β) | Side b |
Side c | a, b, ∠γ | c² = a² + b² - 2ab⋅cos(γ) | Side c |
Angle α | a, b, c | α = cos⁻¹((b² + c² - a²) / 2bc) | Angle α |
Angle β | a, b, c | β = cos⁻¹((a² + c² - b²) / 2ac) | Angle β |
Angle γ | a, b, c | γ = cos⁻¹((a² + b² - c²) / 2ab) | Angle γ |
Table 2 shows the most common work start and end times, along with break durations and corresponding shift types.
How to use Law of Cosines Calculator
This calculator is a very helpful tool to solve triangle problems. Here's how to use this calculator step by step:
1.Choose which you want to calculate a missing side or a missing angle. Choose SAS if you know two sides and the included angle or select SSS if you know all three sides.
2.Enter the sides or angle values into the appropriate fields. Always make sure the values are positive and use consistent units for side measurement.
3.The calculator will apply the law of Cosines formula automatically and provide the result, either the length of the unknown side or unknown angle.
Applications of the Law of Cosines
In many real-life and academic situations in which triangle measurements are important, the Law of Cosines is used. You can use it to solve triangle problems that aren't right-angled, which is very helpful when you can't use Pythagorean Theorem. The following are some popular uses:
1.The law of cosines is most typically utilized in school and college mathematics to solve triangle problems. Especially when students are given two sides plus the included angle (SAS) or all three sides (SSS).
2.Cartography, land surveying, and GPS technology all benefit from its ability to calculate distances across irregular terrain and solve spherical triangles on the Earth's surface.
3.Engineers apply this concept to the design of support beams, bridges, and frames, as well as structural load calculations.
4.Apart from this it is also very helpful in physics and motion analysis, computer graphics and game development, architecture and design.
4 Similar Trigonometry Calculators
Inverse Trig Functions
Graphs Trig Functions
Trig Functions Calculator
Trig Ratios Calculator